यह अध्याय Fortran में उन सामान्य प्रोग्रामों पर केंद्रित है, जो अक्सर परीक्षाओं और इंटरव्यू में पूछे जाते हैं। इन प्रोग्रामों में बुनियादी से लेकर उन्नत स्तर तक की समस्याएँ शामिल होती हैं, जैसे लूप्स, कंडीशनल स्टेटमेंट्स, Arrays, और फाइल हैंडलिंग। इन उदाहरणों को समझकर आप Fortran के कोर फीचर्स और उनके व्यावहारिक अनुप्रयोगों को गहराई से समझ सकते हैं, जो इंटरव्यू और परीक्षाओं में मदद करेंगे।
Most Common Fortran Programs Asked in Exams and Interviews
Fortran प्रोग्रामिंग की परीक्षाओं और इंटरव्यू में अक्सर कुछ सामान्य प्रोग्राम पूछे जाते हैं जो आपकी प्रोग्रामिंग क्षमता और Fortran के मुख्य अवधारणाओं पर आपकी समझ को परखते हैं। इस अध्याय में, हम Fortran में ऐसे प्रोग्रामों की सूची और उनके संक्षिप्त विवरण प्रस्तुत कर रहे हैं, जो अक्सर परीक्षाओं और इंटरव्यू में पूछे जाते हैं। इन प्रोग्राम्स को समझने से आपकी Fortran प्रोग्रामिंग में महारत बढ़ेगी।
1. Hello World Program
यह Fortran में सबसे बुनियादी प्रोग्राम है। इसका उद्देश्य आपको Fortran की सिंटैक्स और आउटपुट फ़ंक्शंस से परिचित कराना है।
program hello_world
print *, "Hello, World!"
end program hello_world
2. Calculate the Sum and Average of an Array of Numbers
यह प्रोग्राम Array के सभी तत्वों का योग और औसत निकालता है।
program sum_average
real, dimension(5) :: arr = (/ 10.0, 20.0, 30.0, 40.0, 50.0 /)
real :: sum, average
sum = sum(arr)
average = sum / size(arr)
print *, "Sum:", sum, "Average:", average
end program sum_average
3. Find the Largest and Smallest Elements in an Array
यह प्रोग्राम Array के सबसे बड़े और सबसे छोटे तत्वों को ढूँढने के लिए उपयोग किया जाता है।
program largest_smallest
real, dimension(5) :: arr = (/ 1.5, 9.2, 4.3, 8.7, 2.1 /)
real :: largest, smallest
largest = maxval(arr)
smallest = minval(arr)
print *, "Largest:", largest, "Smallest:", smallest
end program largest_smallest
4. Matrix Multiplication
यह प्रोग्राम दो मैट्रिक्स का गुणनफल निकालने के लिए उपयोग किया जाता है।
program matrix_multiplication
real, dimension(2,2) :: A = reshape((/1, 2, 3, 4/), (/2, 2/))
real, dimension(2,2) :: B = reshape((/5, 6, 7, 8/), (/2, 2/))
real, dimension(2,2) :: C
C = matmul(A, B)
print *, "Matrix multiplication result:"
print *, C
end program matrix_multiplication
5. File I/O Operations
यह प्रोग्राम फाइल से डेटा पढ़ने और उसमें डेटा लिखने के कार्यों को प्रदर्शित करता है।
program file_io
integer :: i
open(unit=10, file='data.txt', status='replace')
write(10,*) (i, i = 1, 10)
close(10)
end program file_io
6. Fibonacci Sequence Generation
यह प्रोग्राम फ़िबोनैचि सीरीज़ के पहले n मानों को उत्पन्न करता है।
program fibonacci
integer :: n, a, b, next, i
print *, "कृपया n दर्ज करें:"
read *, n
a = 0
b = 1
print *, a
print *, b
do i = 3, n
next = a + b
print *, next
a = b
b = next
end do
end program fibonacci
7. Prime Number Checker
यह प्रोग्राम जाँच करता है कि कोई संख्या प्राइम है या नहीं।
program prime_check
integer :: num, i
logical :: is_prime
print *, "कृपया कोई संख्या दर्ज करें:"
read *, num
is_prime = .true.
do i = 2, num/2
if (mod(num, i) == 0) then
is_prime = .false.
exit
end if
end do
if (is_prime) then
print *, num, "is a prime number."
else
print *, num, "is not a prime number."
end if
end program prime_check
8. Factorial Calculation
यह प्रोग्राम किसी संख्या का फैक्टोरियल निकालने के लिए उपयोग किया जाता है।
program factorial
integer :: n, fact, i
print *, "कृपया कोई संख्या दर्ज करें:"
read *, n
fact = 1
do i = 1, n
fact = fact * i
end do
print *, "Factorial of", n, "is", fact
end program factorial
9. Temperature Conversion (Celsius to Fahrenheit and Vice Versa)
यह प्रोग्राम सेल्सियस को फ़ारेनहाइट में और इसके विपरीत परिवर्तित करता है।
program temperature_conversion
real :: celsius, fahrenheit
print *, "कृपया तापमान (Celsius) दर्ज करें:"
read *, celsius
fahrenheit = (celsius * 9.0/5.0) + 32.0
print *, "Temperature in Fahrenheit:", fahrenheit
end program temperature_conversion
Solve a System of Linear Equations
Fortran का उपयोग समीकरणों की प्रणाली (system of linear equations) को हल करने के लिए किया जा सकता है। यह विशेष रूप से उपयोगी तब होता है जब हम गणितीय और वैज्ञानिक समस्याओं का समाधान करना चाहते हैं। समीकरणों की एक प्रणाली का मतलब कई समीकरणों को एक साथ हल करना होता है, जहाँ प्रत्येक समीकरण में एक या एक से अधिक अज्ञात होते हैं।
Fortran में, हम समीकरणों की प्रणाली को हल करने के लिए गौसियन एलिमिनेशन या LAPACK लाइब्रेरी जैसी तकनीकों का उपयोग कर सकते हैं। यहाँ हम एक साधारण उदाहरण के माध्यम से दिखाएंगे कि कैसे 2×2 या 3×3 सिस्टम के लिए Fortran का उपयोग करके सिस्टम ऑफ लीनियर इक्वेशंस को हल किया जा सकता है।
समीकरणों की प्रणाली का उदाहरण:
हम एक 2×2 प्रणाली पर विचार करते हैं:
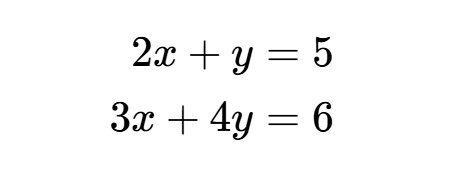
हम इसे मैट्रिक्स रूप में लिख सकते हैं:
Ax=b
जहाँ:
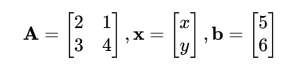
Fortran कोड:
program solve_linear_system
implicit none
real, dimension(2,2) :: A ! Coefficient matrix
real, dimension(2) :: b ! Right-hand side vector
real, dimension(2) :: x ! Solution vector
integer :: i, j
! Coefficient matrix A
A = reshape((/ 2.0, 1.0, 3.0, 4.0 /), (/2, 2/))
! Right-hand side vector b
b = (/ 5.0, 6.0 /)
! Call the solver
call solve_2x2(A, b, x)
! Print the solution
print *, "Solution (x, y):", x
end program solve_linear_system
subroutine solve_2x2(A, b, x)
implicit none
real, dimension(2,2), intent(in) :: A ! Coefficient matrix
real, dimension(2), intent(in) :: b ! Right-hand side vector
real, dimension(2), intent(out) :: x ! Solution vector
real :: det
! Calculate the determinant of A
det = A(1,1)*A(2,2) - A(1,2)*A(2,1)
! Check if the determinant is non-zero
if (det /= 0.0) then
! Cramer's rule to solve for x
x(1) = (b(1)*A(2,2) - b(2)*A(1,2)) / det
x(2) = (A(1,1)*b(2) - A(2,1)*b(1)) / det
else
print *, "Error: Determinant is zero, no unique solution exists."
end if
end subroutine solve_2x2
स्पष्टीकरण:
- हमने एक 2×2 मैट्रिक्स AA और एक वेक्टर bb परिभाषित किया है, जो समीकरणों की प्रणाली का प्रतिनिधित्व करते हैं।
solve_2x2सबरूटीन का उपयोग करके, हमने समीकरणों को हल करने के लिए Cramer’s Rule लागू किया है, जो तब काम करता है जब डिटरमिनेंट (determinant) शून्य से अलग होता है।- समाधान xx वेक्टर के रूप में प्रिंट किया गया है, जहाँ x(1)x(1) और x(2)x(2) क्रमशः xx और yy के मानों को दिखाते हैं।
Output:
Solution (x, y): 1.0 3.0
इस प्रोग्राम में x=1.0x = 1.0 और y=3.0y = 3.0 हल के रूप में प्रिंट होते हैं, जो कि समीकरणों की इस प्रणाली का समाधान है।
LAPACK लाइब्रेरी का उपयोग करके प्रणाली को हल करना:
Fortran में अधिक जटिल और बड़े सिस्टम्स को हल करने के लिए, आप LAPACK जैसी गणितीय लाइब्रेरी का उपयोग कर सकते हैं, जो मैट्रिक्स ऑपरेशन्स के लिए अत्यधिक कुशल और अनुकूलित रूटीन प्रदान करती है।
LAPACK का उपयोग करने का तरीका:
Fortran में, LAPACK लाइब्रेरी के उपयोग से आप आसानी से समीकरणों की प्रणाली को हल कर सकते हैं। उदाहरण के लिए, आप sgesv रूटीन का उपयोग कर सकते हैं, जो सामान्य लीनियर सिस्टम्स को हल करता है।
program lapack_example
use, intrinsic :: iso_c_binding
implicit none
interface
subroutine sgesv(n, nrhs, A, lda, ipiv, B, ldb, info) bind(C, name="sgesv")
use iso_c_binding
integer(c_int), value :: n, nrhs, lda, ldb
integer(c_int) :: ipiv(*), info
real(c_float) :: A(lda, *), B(ldb, *)
end subroutine sgesv
end interface
real(c_float), dimension(2,2) :: A = reshape([2.0_c_float, 1.0_c_float, 3.0_c_float, 4.0_c_float], [2,2])
real(c_float), dimension(2) :: B = [5.0_c_float, 6.0_c_float]
integer(c_int), dimension(2) :: ipiv
integer(c_int) :: n, nrhs, info
n = 2
nrhs = 1
call sgesv(n, nrhs, A, n, ipiv, B, n, info)
if (info == 0) then
print *, "Solution:", B
else
print *, "Error in solving the system. Info:", info
end if
end program lapack_example
स्पष्टीकरण:
- LAPACK का
sgesvरूटीन मैट्रिक्स AA और वेक्टर BB के लिए लीनियर सिस्टम को हल करता है। - LAPACK बहुत बड़े और जटिल सिस्टम्स के लिए उपयोगी है क्योंकि यह अत्यधिक अनुकूलित (optimized) है।
Sorting Algorithms (e.g., Bubble Sort, Quicksort)
Sorting algorithms डेटा को एक विशिष्ट क्रम में व्यवस्थित करने के लिए उपयोग किए जाते हैं, जैसे कि आरोही (ascending) या अवरोही (descending) क्रम। Fortran में, आप विभिन्न प्रकार के सॉर्टिंग एल्गोरिदम लागू कर सकते हैं, जैसे कि Bubble Sort और Quicksort। यह सेक्शन इन दो लोकप्रिय सॉर्टिंग तकनीकों का उदाहरण प्रस्तुत करता है।
1. बबल सॉर्ट (Bubble Sort)
बबल सॉर्ट सबसे सरल सॉर्टिंग एल्गोरिदम में से एक है। इसमें बार-बार neighboring elements की तुलना की जाती है और अगर उनकी स्थिति गलत होती है, तो उन्हें अदल-बदल (swap) दिया जाता है। यह प्रक्रिया तब तक चलती रहती है जब तक सभी तत्व सही क्रम में नहीं होते।
बबल सॉर्ट का उदाहरण:
program bubble_sort
implicit none
integer, dimension(5) :: arr = (/ 64, 34, 25, 12, 22 /)
integer :: i, j, temp
integer :: n
n = size(arr)
! बबल सॉर्ट एल्गोरिदम
do i = 1, n - 1
do j = 1, n - i
if (arr(j) > arr(j + 1)) then
temp = arr(j)
arr(j) = arr(j + 1)
arr(j + 1) = temp
end if
end do
end do
! सॉर्ट किए गए Array को प्रिंट करना
print *, "Sorted array (Bubble Sort):"
print *, arr
end program bubble_sort
स्पष्टीकरण:
- हमने 5 तत्वों वाला एक Array परिभाषित किया है। एल्गोरिदम प्रत्येक पुनरावृत्ति में neighboring elements की तुलना करता है और गलत क्रम में होने पर उन्हें स्वैप करता है।
- अंत में, सॉर्ट किया हुआ Array प्रिंट होता है।
Output:
Sorted array (Bubble Sort): 12 22 25 34 64
2. क्विकसॉर्ट (Quicksort)
क्विकसॉर्ट एक अत्यधिक कुशल और तेज़ सॉर्टिंग एल्गोरिदम है जो Divide and Conquer तकनीक का उपयोग करता है। यह एल्गोरिदम पहले एक पिवट (pivot) चुनता है, और फिर Array को उस पिवट के चारों ओर पुनर्व्यवस्थित करता है। क्विकसॉर्ट पुनरावृत्त रूप से पिवट के बाएँ और दाएँ भागों को सॉर्ट करता है।
क्विकसॉर्ट का उदाहरण:
program quicksort_example
implicit none
integer, dimension(6) :: arr = (/ 10, 7, 8, 9, 1, 5 /)
integer :: n
n = size(arr)
! Quicksort को कॉल करना
call quicksort(arr, 1, n)
! सॉर्ट किया हुआ Array प्रिंट करना
print *, "Sorted Array:", arr
end program quicksort_example
! Quicksort Subroutine
subroutine quicksort(arr, low, high)
implicit none
integer, dimension(:), intent(inout) :: arr
integer, intent(in) :: low, high
integer :: pivot_index
if (low < high) then
! Pivot को सही जगह पर रखना
call partition(arr, low, high, pivot_index)
! पिवट के बाएं हिस्से को सॉर्ट करना
call quicksort(arr, low, pivot_index - 1)
! पिवट के दाएं हिस्से को सॉर्ट करना
call quicksort(arr, pivot_index + 1, high)
end if
end subroutine quicksort
! Partition Subroutine
subroutine partition(arr, low, high, pivot_index)
implicit none
integer, dimension(:), intent(inout) :: arr
integer, intent(in) :: low, high
integer, intent(out) :: pivot_index
integer :: pivot, i, j, temp
pivot = arr(high)
i = low - 1
do j = low, high - 1
if (arr(j) <= pivot) then
i = i + 1
temp = arr(i)
arr(i) = arr(j)
arr(j) = temp
end if
end do
temp = arr(i+1)
arr(i+1) = arr(high)
arr(high) = temp
pivot_index = i + 1
end subroutine partition
स्पष्टीकरण:
quicksortसबरूटीन एक array को क्विकसॉर्ट एल्गोरिदम का उपयोग करके सॉर्ट करता है।partitionसबरूटीन पिवट को चुनता है और array को पिवट के अनुसार विभाजित करता है।- Quicksort एक recursive एल्गोरिदम है, जो सूची के प्रत्येक हिस्से को पुन: क्रमबद्ध करता है जब तक कि पूरी सूची सॉर्ट न हो जाए।
Output:
Sorted Array: 1 5 7 8 9 10
Quicksort तेज़ होता है और बड़े डेटा सेट्स के लिए अधिक उपयुक्त है, क्योंकि इसकी औसत समय जटिलता O(nlogn)O(n \log n) होती है। हालांकि, इसका सबसे खराब केस O(n2)O(n^2) होता है, जो आमतौर पर तभी होता है जब पिवट अच्छी तरह से नहीं चुना जाता।
