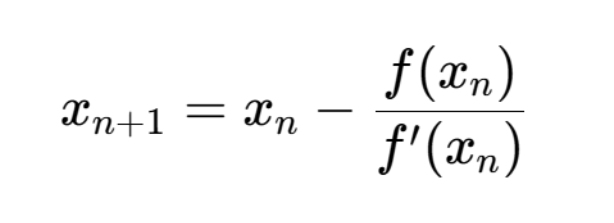इस अध्याय में, हम Fortran प्रोग्रामिंग के व्यावहारिक उदाहरणों पर ध्यान देंगे। ये उदाहरण आपको Fortran की विभिन्न तकनीकों और फीचर्स को वास्तविक समस्याओं को हल करने में कैसे उपयोग किया जा सकता है, यह सिखाएंगे। इन प्रैक्टिकल उदाहरणों में गणितीय गणनाएँ, डेटा प्रोसेसिंग, और वैज्ञानिक सिमुलेशन जैसे महत्वपूर्ण विषय शामिल होंगे। ये उदाहरण आपके कौशल को मजबूत करने और Fortran में जटिल प्रोग्राम्स को समझने में मदद करेंगे।
Scientific Computations
Fortran प्रोग्रामिंग भाषा वैज्ञानिक और तकनीकी गणनाओं के लिए एक महत्वपूर्ण उपकरण है। इसकी उच्च सटीकता और गणना करने की क्षमता इसे वैज्ञानिक समस्याओं को हल करने के लिए आदर्श बनाती है। इस सेक्शन में, हम Fortran का उपयोग करके एक साधारण वैज्ञानिक गणना कैसे करें, यह जानेंगे। उदाहरण के तौर पर, हम न्यूटन के गति के दूसरे नियम पर आधारित एक सरल गणना करेंगे।
Fortran में एक साधारण वैज्ञानिक गणना:
विज्ञान और इंजीनियरिंग में गणनाएँ महत्वपूर्ण होती हैं। एक आम गणना न्यूटन के गति के दूसरे नियम F=m×aF = m \times a के माध्यम से बल की गणना करना है, जहाँ:
- FF बल है,
- mm द्रव्यमान (mass) है,
- aa त्वरण (acceleration) है।
उदाहरण: वस्तु पर लगने वाला बल (Force) की गणना:
program force_calculation
real :: mass, acceleration, force
! यूज़र से द्रव्यमान और त्वरण का इनपुट लेना
print *, "कृपया वस्तु का द्रव्यमान (kg) दर्ज करें:"
read *, mass
print *, "कृपया त्वरण (m/s^2) दर्ज करें:"
read *, acceleration
! बल की गणना: F = m * a
force = mass * acceleration
! परिणाम प्रिंट करना
print *, "वस्तु पर लगने वाला बल है:", force, "न्यूटन"
end program force_calculation
स्पष्टीकरण:
- प्रोग्राम यूज़र से वस्तु का द्रव्यमान (mass) और त्वरण (acceleration) इनपुट करता है।
- इसके बाद न्यूटन के गति के दूसरे नियम F=m×aF = m \times a का उपयोग करके बल (force) की गणना की जाती है।
- बल की गणना के बाद, परिणाम को न्यूटन (N) में प्रदर्शित किया जाता है।
गणितीय फ़ंक्शंस का उपयोग:
Fortran में कई गणितीय फ़ंक्शंस उपलब्ध हैं, जिनका उपयोग वैज्ञानिक गणनाओं में किया जा सकता है। कुछ महत्वपूर्ण फ़ंक्शंस हैं:
- sqrt(x): xx का वर्गमूल निकालने के लिए।
- exp(x): exe^x की गणना के लिए।
- log(x): प्राकृतिक लॉगरिदम (logarithm) के लिए।
- sin(x), cos(x), tan(x): ट्रिग्नोमेट्रिक फ़ंक्शंस।
- abs(x): xx का परिमाण (absolute value) निकालने के लिए।
उदाहरण: किसी संख्या का वर्गमूल (Square Root) निकालना:
program square_root_calculation
real :: number, result
! यूज़र से संख्या लेना
print *, "कृपया कोई संख्या दर्ज करें:"
read *, number
! वर्गमूल की गणना
result = sqrt(number)
! परिणाम प्रिंट करना
print *, "संख्या का वर्गमूल है:", result
end program square_root_calculation
स्पष्टीकरण:
- इस प्रोग्राम में
sqrtफ़ंक्शन का उपयोग किसी संख्या का वर्गमूल निकालने के लिए किया गया है। - यूज़र से एक संख्या ली जाती है और उसका वर्गमूल प्रिंट किया जाता है।
विज्ञान में Fortran का उपयोग:
Fortran वैज्ञानिक गणनाओं के लिए व्यापक रूप से उपयोग की जाने वाली भाषा है। इसका उपयोग विभिन्न क्षेत्रों में किया जाता है, जैसे:
- यांत्रिकी (Mechanics): बल, गति, और ऊर्जा जैसी गणनाएँ।
- भौतिकी (Physics): विद्युत, चुंबकीय क्षेत्र और कणों की गति का अध्ययन।
- रसायन विज्ञान (Chemistry): रासायनिक प्रतिक्रियाओं का मॉडलिंग और अणुओं की संरचना।
- जलवायु मॉडलिंग (Climate Modeling): जलवायु परिवर्तन और मौसम की भविष्यवाणी के लिए।
Numerical Methods
Fortran का उपयोग व्यापक रूप से गणितीय समस्याओं को हल करने के लिए Numerical Methods के कार्यान्वयन में किया जाता है। Numerical Methods का उद्देश्य गणितीय समीकरणों का सटीक या अनुमानित हल निकालने के लिए संख्यात्मक दृष्टिकोण का उपयोग करना है। Fortran की सटीकता और कुशल गणना क्षमताओं के कारण यह वैज्ञानिक और इंजीनियरिंग समस्याओं को हल करने के लिए एक लोकप्रिय भाषा है। इस सेक्शन में, हम Fortran का उपयोग करके कुछ सामान्य Numerical Methods को लागू करेंगे, जैसे कि बाइसेक्शन मेथड (Bisection Method) और न्यूटन-रफसन मेथड (Newton-Raphson Method)।
1. बाइसेक्शन मेथड (Bisection Method):
बाइसेक्शन मेथड एक सरल और विश्वसनीय तकनीक है जो किसी निरंतर फलन f(x)f(x) के मूल (root) को ढूंढने के लिए उपयोग की जाती है। इस मेथड में, आपको एक इंटरवल [a, b] चुनना होता है जहाँ f(a)f(a) और f(b)f(b) के संकेत विपरीत होते हैं। इसके बाद, इंटरवल को आधा करके मूल का अनुमान लगाया जाता है, और यह प्रक्रिया तब तक दोहराई जाती है जब तक मूल नहीं मिल जाता।
बाइसेक्शन मेथड का उदाहरण:
program bisection_method
implicit none
real :: a, b, mid, tol
integer :: max_iter, i
external :: func
! इंटरवल और अन्य प्रारंभिक मान
a = 1.0
b = 2.0
tol = 0.0001
max_iter = 100
! बाइसेक्शन मेथड का कार्यान्वयन
do i = 1, max_iter
mid = (a + b) / 2.0
if (abs(func(mid)) < tol) then
print *, "मूल (root) है:", mid
exit
elseif (func(a) * func(mid) < 0.0) then
b = mid
else
a = mid
end if
end do
end program bisection_method
! फलन (Function) f(x) = x^2 - 2
real function func(x)
real :: x
func = x**2 - 2.0
end function func
स्पष्टीकरण:
- यहाँ, बाइसेक्शन मेथड का उपयोग f(x)=x2−2f(x) = x^2 – 2 के लिए किया गया है। इसका हल 2\sqrt{2} है।
midइंटरवल का मध्य बिंदु है, और जब तक फलन का मान छोटे ϵ\epsilon (tolerance) से छोटा नहीं हो जाता, तब तक प्रक्रिया जारी रहती है।
2. न्यूटन-रफसन मेथड (Newton-Raphson Method):
न्यूटन-रफसन मेथड एक तेज़ और कुशल तकनीक है जो किसी निरंतर फलन f(x)f(x) के मूल को खोजने के लिए उपयोग की जाती है। इस मेथड में, प्रारंभिक अनुमान x0x_0 से शुरू करके f(x)f(x) का रेखीय सन्निकटन (linear approximation) किया जाता है और धीरे-धीरे मूल का सटीक मान निकाला जाता है। यह निम्नलिखित समीकरण पर आधारित है:
न्यूटन-रफसन मेथड का उदाहरण:
program newton_raphson_method
implicit none
real :: x0, x1, tol
integer :: max_iter, i
external :: func, func_derivative
! प्रारंभिक अनुमान और सहनशीलता (tolerance)
x0 = 1.0
tol = 0.0001
max_iter = 100
! न्यूटन-रफसन मेथड का कार्यान्वयन
do i = 1, max_iter
x1 = x0 - func(x0) / func_derivative(x0)
if (abs(x1 - x0) < tol) then
print *, "मूल (root) है:", x1
exit
endif
x0 = x1
end do
end program newton_raphson_method
! फलन (Function) f(x) = x^2 - 2
real function func(x)
real :: x
func = x**2 - 2.0
end function func
! फलन का डेरिवेटिव f'(x) = 2*x
real function func_derivative(x)
real :: x
func_derivative = 2.0 * x
end function func_derivative
स्पष्टीकरण:
- इस उदाहरण में, न्यूटन-रफसन मेथड का उपयोग f(x)=x2−2f(x) = x^2 – 2 के लिए किया गया है, जिसका हल 2\sqrt{2} है।
funcऔरfunc_derivativeक्रमशः फलन और उसका डेरिवेटिव हैं। हर पुनरावृत्ति में x0x_0 का मान अद्यतन होता है जब तक कि सहनशीलता (tolerance) पूरी नहीं होती।
Numerical Methods का उपयोग:
Numerical Methods का उपयोग विभिन्न क्षेत्रों में किया जाता है, जैसे:
- जड़ (Roots) खोजने के लिए: जैसे कि बाइसेक्शन, न्यूटन-रफसन मेथड।
- डिफरेंशियल समीकरण हल करने के लिए: रंके-कुट्टा मेथड (Runge-Kutta method), यूलेर की विधि (Euler’s method)।
- समीकरणों की प्रणाली: Gauss-Seidel मेथड, LU Decomposition।
- इंटीग्रेशन और डिफरेंशिएशन: ट्रैपेज़ॉइडल मेथड (Trapezoidal method), सिम्पसन का नियम (Simpson’s rule)।
Projects
Fortran में प्रोजेक्ट बनाना आपकी प्रोग्रामिंग क्षमताओं को वास्तविक दुनिया की समस्याओं पर लागू करने का एक शानदार तरीका है। इस सेक्शन में, हम Fortran में एक छोटा प्रोजेक्ट बनाएंगे जो आपको संख्यात्मक गणनाओं और वैज्ञानिक अनुप्रयोगों के लिए Fortran का उपयोग करने का तरीका समझने में मदद करेगा। इस प्रोजेक्ट का उद्देश्य Fortran के विभिन्न फीचर्स, जैसे कि फाइल हैंडलिंग, गणितीय फ़ंक्शंस, और डेटा प्रोसेसिंग का व्यावहारिक उपयोग दिखाना है।
Fortran में एक छोटा प्रोजेक्ट: गणितीय डेटा का विश्लेषण
इस प्रोजेक्ट का उद्देश्य फाइल से डेटा पढ़ना, उस डेटा पर गणितीय विश्लेषण करना, और परिणाम को फाइल में आउटपुट करना है। यह प्रोजेक्ट एक वैज्ञानिक डेटा सेट पर औसत (average), मानक विचलन (standard deviation), और अधिकतम/न्यूनतम मानों की गणना करेगा।
प्रोजेक्ट का विवरण:
हमारे पास एक फाइल data.txt है, जिसमें विभिन्न मापों के मान (values) हैं। हमारा उद्देश्य इन मानों पर गणितीय विश्लेषण करना और आउटपुट को एक नई फाइल में सहेजना है।
डेटा इनपुट फाइल (data.txt):
12.5 15.2 9.8 11.7 14.3 18.0 10.6
प्रोजेक्ट का कोड:
program data_analysis
implicit none
real, dimension(:), allocatable :: data
real :: avg, stddev, maxval, minval
integer :: n, i
character(len=100) :: filename
real :: sum, sumsq, variance
! डेटा फाइल का नाम और फाइल से डेटा पढ़ना
filename = 'data.txt'
open(unit=10, file=filename, status='old')
! डेटा की संख्या गिनना
n = 0
do
read(10, *, iostat=i)
if (i /= 0) exit
n = n + 1
end do
! डेटा के लिए मेमोरी एलोकेट करना और फिर से फाइल से डेटा पढ़ना
rewind(10)
allocate(data(n))
do i = 1, n
read(10, *) data(i)
end do
close(10)
! औसत (Average) की गणना
sum = 0.0
do i = 1, n
sum = sum + data(i)
end do
avg = sum / n
! मानक विचलन (Standard Deviation) की गणना
sumsq = 0.0
do i = 1, n
sumsq = sumsq + (data(i) - avg)**2
end do
variance = sumsq / (n - 1)
stddev = sqrt(variance)
! अधिकतम और न्यूनतम मानों की गणना
maxval = maxval(data)
minval = minval(data)
! परिणामों को फाइल में लिखना
open(unit=20, file='results.txt', status='replace')
write(20, *) "डेटा का विश्लेषण:"
write(20, *) "औसत:", avg
write(20, *) "मानक विचलन:", stddev
write(20, *) "अधिकतम मान:", maxval
write(20, *) "न्यूनतम मान:", minval
close(20)
! मेमोरी को मुक्त करना
deallocate(data)
print *, "डेटा का विश्लेषण पूरा हो गया। परिणाम 'results.txt' में सहेजे गए हैं।"
end program data_analysis
स्पष्टीकरण:
- डेटा पढ़ना: सबसे पहले,
data.txtसे डेटा पढ़ा जाता है, और डेटा की संख्या का अनुमान लगाया जाता है। इसके बाद, उस डेटा को एक एलोकेटेबल Array में स्टोर किया जाता है। - गणनाएँ:
- औसत (Average) निकालने के लिए, सभी मानों का योग लेकर उसे संख्या के साथ विभाजित किया जाता है।
- मानक विचलन (Standard Deviation) निकालने के लिए, पहले विचलन (variance) की गणना की जाती है और फिर उसका वर्गमूल लिया जाता है।
- अधिकतम और न्यूनतम मान
maxvalऔरminvalफ़ंक्शन के माध्यम से निकाले जाते हैं।
- आउटपुट फाइल में लिखना: गणनाओं के परिणामों को
results.txtनामक फाइल में लिखा जाता है। - मेमोरी प्रबंधन: डेटा के लिए एलोकेट की गई मेमोरी को अंत में
deallocateकिया जाता है।
आउटपुट फाइल (results.txt):
डेटा का विश्लेषण: औसत: 13.442857 मानक विचलन: 2.804620 अधिकतम मान: 18.000000 न्यूनतम मान: 9.800000
प्रोजेक्ट के उद्देश्य:
- फ़ाइल हैंडलिंग: इस प्रोजेक्ट में Fortran के फ़ाइल हैंडलिंग फीचर्स का उपयोग किया गया है, जहाँ डेटा को पढ़ा और लिखा जाता है।
- गणितीय विश्लेषण: औसत, मानक विचलन, और अधिकतम/न्यूनतम मानों की गणना दिखाती है कि कैसे Fortran का उपयोग डेटा विश्लेषण के लिए किया जा सकता है।
- डायनामिक मेमोरी एलोकेशन: डेटा की लंबाई ज्ञात करने के बाद मेमोरी को डायनामिक रूप से एलोकेट किया गया है।